【クイズ】コーヒーとミルクの問題を図解で理解する

はじめに

コーヒーとミルクという論理クイズがありますが、直観に反する事象のため、有無を言わせず納得させるべく数式にして解説しました。

ただ、本質的な理解をするためには数式は不要で図示すると肝が掴めます。
本記事では、この問題を図に落とし込むことで数字を使わず回答に近づきます。

問題と解答

2つのカップA,Bがある。
Aにはミルクが、Bにはコーヒーが入っている。
いま、AのミルクをスプーンですくってBに移し、Bをよくかきまぜる。
その後、さきほどと同じ量だけBの液体をスプーンですくってAに移す。

このとき、Aの中にあるコーヒーの量は、Bの中にあるミルクの量より多いだろうか？

という頭の体操です。で、答えは同じ量です。

要は、ブラックのコーヒーにミルク入れからスプーン一杯のミルクを入れ、そのコーヒーをスプーン一杯に取り出すとそのスプーンに入っているコーヒーの量とコーヒーカップに残ったミルクの量が同じという不思議な話です。

スポンサーリンク

図で理解する

問題の性質上、ミルクしか入っていないAに入ってくるコーヒーの量だけが知りたいので、もともとミルクが何グラムかは情報として全く必要がない点がポイントです。

AのミルクをスプーンですくってBに移し、Bをよくかきまぜる

スプーン一杯のミルクとブラックコーヒー

こちらをBに入れてよくかきまぜると以下になります。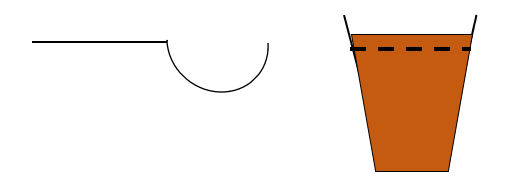

ミルクの分だけ嵩が増えたコーヒー

さきほどと同じ量だけBの液体をスプーンですくってAに移す

スプーン一杯分を回収する

今回は本質ではないので、元のミルク容器に戻すことはしません。

上の図で言うところのスプーン側に入っているコーヒーとB側に入っているミルクの量の大小が問題です。

混ざっているコーヒーとミルクを分離すると分りやすい

混ざっているものを分離して見る

上記図を見ると、もともとスプーン一杯がミルクだった以下の図と比較すると

スプーン内に余分にコーヒーが含まれています。

ではもともとミルクが含まれていた分はどこにいったのでしょうか。

それは右側にいます。スプーンにコーヒーを入れることで溢れてしまったミルクがBのコップにこぼれたと考えると分かりやすいです。

スポンサーリンク

補足

この図を見れば「Bをよくかきまぜる」必要がないことが分かります。
本質として、スプーンから溢れたミルクとスプーンに入り込んだコーヒーの量は等しいというのが肝で、Bの濃度が一定である状態は問題の性質上求められていません。

以下のように濃度の計算式を用いて数式に落とし込むこと自体が「よくかきませる」に翻弄されているようにも思えます。

要は、均一になりきる手前でスプーンですくっても、やはりスプーンにコーヒーが入りこんだ分だけコップBにミルクが入ってしまい、量は等しいのです。

終わりに

計算式で導出した際は混ざりきることで濃度が均質であるという前提を利用しましたが、本記事を見ればその前提すら不要であることが掴めると思います。そういう意味では、中学数学すら使わずに解けてしまう問題ということで、よくできていると思います

以上、ご参考になれば幸いです。