【R言語】セルオートマトン入門とその描画

はじめに

以下のような画像を見たことはあるでしょうか。
f:id:mtiit:20190521220523p:plain
こちらはシェルピンスキーのギャスケットと呼ばれるフラクタル図形ですが、
「二状態・三近傍・一次元セルオートマトン」として生成することができます。

本記事では、セルオートマトンとはなにか　と　それを描画するためのコード　について解説します。

セルオートマトン？

セルオートマトンとは内部状態を持ったセル（格子）が他のセルとの相互作用によって時間的に変化していくモデルです。

冒頭で述べた「二状態・三近傍・一次元セルオートマトン」とは「次の状態が白か黒かは現在の自分と両隣のセルの状態で決まる一列に並んだセル」を意味します。

このオートマトンですが、状態の更新ルールと初期状態を決めてしまえば、任意の時刻のセルの状態が算出できます。

例えば以下のような状態更新ルールを策定します。
f:id:mtiit:20181205121638p:plain
見方は真ん中のセルに着目し

自分と左右の状態を確認し、黒が１～２つあれば次の状態は黒
自分と左右の状態を確認し、全て白または全て黒なら次の状態は白

を意味しています。

プログラミング風に書くと以下の条件式です

if(cell[i-1,t]+cell[i,t]+cell[i+1,t] > 0 && cell[i-1,t]+cell[i,t]+cell[i+1,t] <3)
{
 cell[i,t+1] = 1;
}
else
{
 cell[i,t+1] = 0;
}

実は冒頭で見せた画像も上記ルールに従って描画されています。

セルオートマトンのおもしろさは、描き出される複雑な模様が単純な入力情報にて生成される点にあります。

これは、ライフゲーム、つまり生物の誕生/死滅を単純化したシミュレーションにも利用されます。
先ほどのルールは見方を変えれば「過疎（周りが全て白）」または「過密（周りが全て黒）」なら次世代は死滅状態になるという条件です。

R言語にて描画

まずはR言語にてspパッケージをインストールします。

> install.packages("sp")
trying URL 'https://cran.rstudio.com/bin/windows/contrib/3.4/sp_1.3-1.zip'
Content type 'application/zip' length 1538931 bytes (1.5 MB)
downloaded 1.5 MB
package ‘sp’ successfully unpacked and MD5 sums checked
The downloaded binary packages are in
	C:\Users\XXXX\AppData\Local\Temp\RtmpcRvWH9\downloaded_packages

そして以下のサンプルコード( https://www.r-bloggers.com/cellular-automata-the-beauty-of-simplicity/ より抜粋 )を利用すれば８セルのセルオートマトンが描画できます。

library(sp)
width <-2^3
depth <-width/2
gt = GridTopology(cellcentre=c(1,1),cellsize=c(1,1),cells=c(width, depth))
s_gt = SpatialGrid(gt)
z <- data.frame(status=sample(0:0, width, replace=T))
z[width/2, 1] <- 1
z[width/2+1, 1] <- 1
for (i in (width+1):(width*depth))
{
  ilf <- i-width-1
  iup <- i-width
  irg <- i-width+1
  if (i%%width==0) irg <- i-2*width+1
  if (i%%width==1) ilf <- i-1
  if((z[ilf,1]+z[iup,1]+z[irg,1]>0)&(z[ilf,1]+z[iup,1]+z[irg,1]<3))
    {st <- 1}
  else 
    {st <- 0}
  nr<-as.data.frame(st)
  colnames(nr)<-c("status")
  z<-rbind(z,nr)
}
sgdf = SpatialGridDataFrame(s_gt, z)
image(sgdf, col=c("white", "black"))

出力結果は以下となります。
f:id:mtiit:20190518230928p:plain

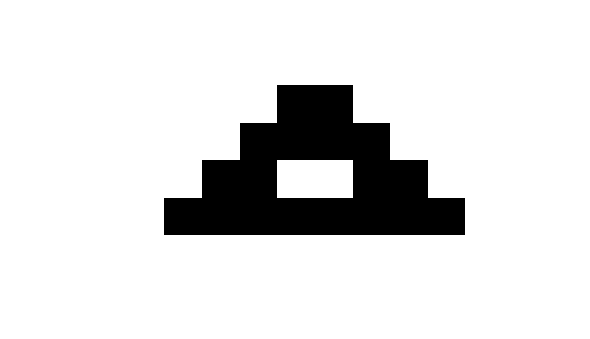
解説ですが、初期条件は中央の２セルのみ黒です。

z[width/2, 1] <- 1
z[width/2+1, 1] <- 1

そして上で述べたルールに従い生誕/死滅を行います。

0	0	0	1	1	0	0	0

は次の状態にて

0	0	1	1	1	1	0	0

は次の状態にて（過密が中央で発生）

0	1	1	0	0	1	1	0

は次の状態にて

1	1	1	1	1	1	1	1

となります。これに白黒を対応させれば確かに上の画像と一致します。

この描画を大きくしたければ以下の「3」の箇所を大きくします。指数関数的に計算量が増加するので値の設定はご注意ください。

width <-2^3

初期条件をランダムにしてみると

width <-2^7

とし

z <- data.frame(status=sample(floor(runif(2^7, min=0, max=2)), width, replace=T))

以下のようになります。綺麗です。
f:id:mtiit:20190522145041p:plain

終わりに

セルオートマトンとは元来はコンピュータによる遊びですが、簡単なルールの中でも複雑な状況が出現するところにおもしろさがあります。生誕/死滅の条件を変えたり、初期状態を変えれば模様も変化します。

冒頭のような画像を見た際に「これは上部から下部に向かって時刻毎の状態を表しており、その状態は初期値と状態変化のルールによって算出される」といったことを連想できれば、本記事の目的達成です。

以上、セルオートマトンの入門記事でした。

(O+P)ut

アウトプット