【セルオートマトン】ランダム性を持つルール30を描画する

はじめに

以下の記事にて二状態・三近傍・一次元セルオートマトンの簡単な解説を行い、記事の中でフラクタル図形を生成しました。

一方で、セルオートマトンの状態変化のルールによってはセルの状態にランダム性・カオス性が見られます。

ランダム（英語: random）とは、事象の発生に法則性（規則性）がなく、予測が不可能な状態である。

カオス（英語: chaos）とは、初期値のわずかな変化で予想が不可能な不規則現象を引き起こす状態である。

本記事では、ルール30という用語を説明し、描画しながらランダム性を見ていきます。

ルール30

三近傍のセルオートマトンでは、左のセルの状態、真ん中のセルの状態、右のセルの状態で次のセルの状態が決まります。要は、３つの並んだセルの計８状態に対してそれぞれの出力である白か黒かを指定する必要があります。

つまり、ルールの総数は256通りとなります。

> 2^8
[1] 256

256通りの中の一つに以下ルールがあります。

現在の状態	中央セルの次状態
111	0
110	0
101	0
100	1
011	1
010	1
001	1
000	0

この出力結果である00011110を2進数として見れば「30」を意味します。

> 2^4 + 2^3 + 2^2 + 2^1
[1] 30

よってこの条件をルール30と呼びます。

プログラミング風に書くと以下となります。

if(cell[i-1,t]+cell[i,t]+cell[i+1,t] == 1 || cell[i-1,t]+2*cell[i,t]+4*cell[i+1,t] ==6)
{
 cell[i,t+1] = 1;
}
else
{
 cell[i,t+1] = 0;
}

中央の2セルのみ1でスタートした際の図形模様を見てみます。

描画例

8セル

f:id:mtiit:20190521092256p:plain
（３つのセルで1が一つまたは中央と右が1 の場合は1）

0	0	0	1	1	0	0	0
0	0	1	1	0	1	0	0
0	1	1	0	0	1	1	0
1	1	0	1	1	1	0	1

確かに上の画像と一致します。

16セル

f:id:mtiit:20190521092308p:plain
まだ複雑性は見られません。

64セル

f:id:mtiit:20190521092319p:plain
左側は規則正しいですが、右側は何かの繰り返しにはなっていません。

256セル

f:id:mtiit:20190521100049p:plain
ところどころ白い逆三角形が目につきますが、規則性はなさそうです。

1024セル

f:id:mtiit:20190521095613p:plain
濃淡でしか見れませんが、規則性はなさそうです。

GIF

セルオートマトンの描画範囲を順々に大きくしていくGif画像は下記になります。
f:id:mtiit:20190521092439g:plain

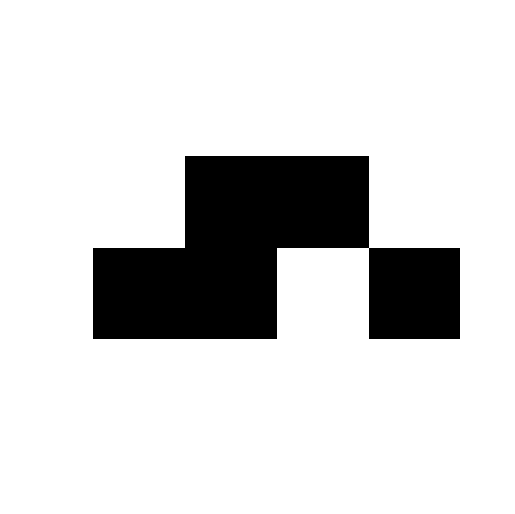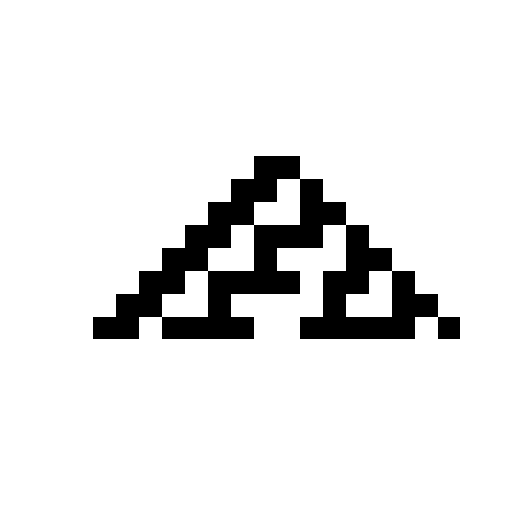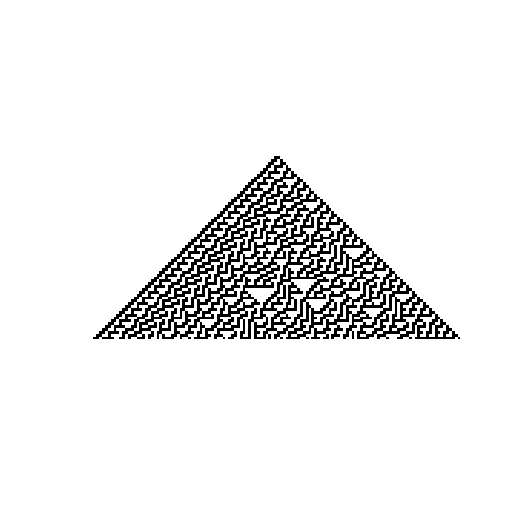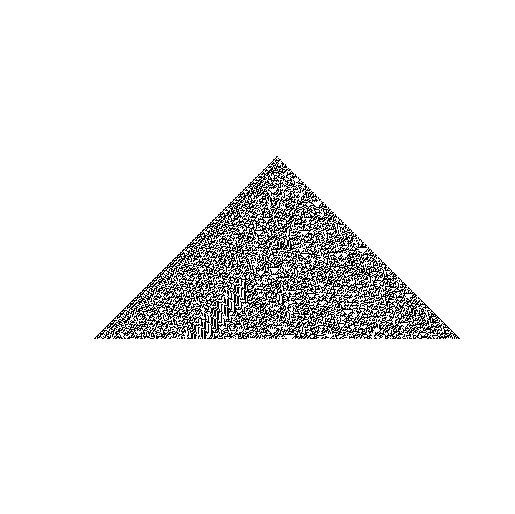
ランダム性

このルール30は、スティーブン・ウルフラムの４つの分類としては「非線形系・カオス」にあたります。

実際、ルール３０はカオスの性質の一つである、初期条件のわずかな変化で出力が大きく変化する初期値敏感性(sensitivity to initial conditions)を持っているようです。

試しに初期条件に同じ乱数が発生するようにし

set.seed(101)
z <- data.frame(status=sample(floor(runif(2^7, min=0, max=2)), width, replace=T))

中心の一セルのみ値を反転させました。

z[width/2, 1] <- 0

その出力結果の差異は以下になります。他のルールでも変化はあるものの1ビットの変化で図形はガラッと変わります。
f:id:mtiit:20190522150451g:plain

終わりに

シンプルなルールにて深淵な図が出来上がる大変興味深い現象なので、実際にR言語で描画してみました。

以上です。

(O+P)ut

アウトプット