
はじめに
ぽあそん?分布?
程度の知識でもポアソン分布について理解できるよう、順を追って説明する入門記事を書いてみました。
所要時間目安 : 10分
ポアソン分布って?
ポアソン分布(Poisson distribution)とは、数学者ポアソン氏が発表した確率分布で、滅多に起こらない現象が離散的に発生する事象を扱えます。
離散的ってどういうこと?
事象が連続値でないことを指しています。例えば温度のような値は連続的ですが、ホームページへのアクセス数は連続的ではありません。1PV、2PVはあっても1.4PVなんてないですよね。このように飛び飛びで観測されるものは「離散的」です。
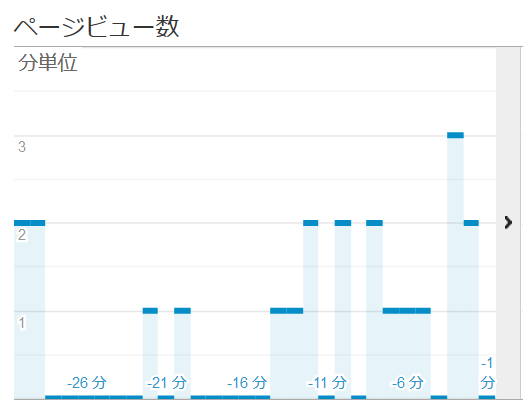
よくあるポアソン分布でモデル化できる例ですが
- ある一定の時間内に特定の交差点を通過する車両の台数
- ある一定の時間内の電話がかかってくる件数。
- ある一定の時間内の店への来客数。
等です。全て離散的な値を扱っています。
ポアソン分布の特徴
ポアソン分布でモデル化できると何が嬉しいの?
ポアソン分布の特徴は一定期間に起こる現象の発生回数の平均値さえ決めてあげれば分布図を書ける点にあります。例えば1分あたり平均2人がアクセスするホームページに対して1分あたりN人がアクセスに来る確率が分かります。1分あたり5人アクセスが来るのは滅多に起きないですが、それがどれくらい滅多に起きないかを数値で表現できます。
そんなに珍しい特徴なの?
平均値さえ決めてあげれば分布図が書ける性質はかなりユニークです。
一例ですがクラスのテストの平均点だけ分かってもクラス全体の点数の分布は分かりません。
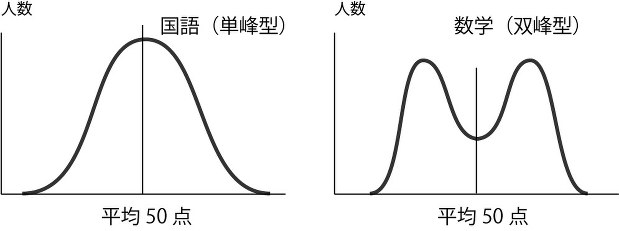
一方、ポアソン分布では分布まで分かってしまいます。
つまり「ある期間に平均してX回起こる現象が、ある期間にちょうどY回起きる確率」が分かります。
滅多に起こらない現象を一定の期間観測するという特別ケースのみに適用可能な分布なのでテストの点数分布には利用できませんが、1秒あたりのアクセス数はほぼ0でも60秒観測すると平均で2件のアクセスがあるといった特別な事象には利用できます。
ちなみに分布としてはどんな数式で表現されるの?
式自体は以下になります。式に興味がある方は二項分布からの導出できるのではぜひ調べてみてください。
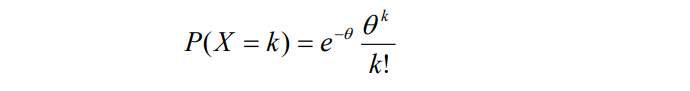
θ?K?...
θは事象の平均発生回数です。例えば、1分間で2回発生する事象であればθは2となります。
Kは事象の発生回数です。事象が4回発生する確率が知りたければ上記数式に4を入れて関数電卓を叩けば数値が出ます。
世に色んな分布がありますが、平均値のみで決まる分布というのはとても珍しく、この単純さより確率分布の分野では入門として最初に取り上げられることが多いです。
グラフ化してみる
θが1、2、3、5としてKが0~10をとる場合をポアソン分布dpois関数で可視化してみます。
横軸がKの値で、縦軸がそのKが発生する確率です。
0から始まるため、Index-1がKと思ってください。
> plot(dpois(c(0:10),1))
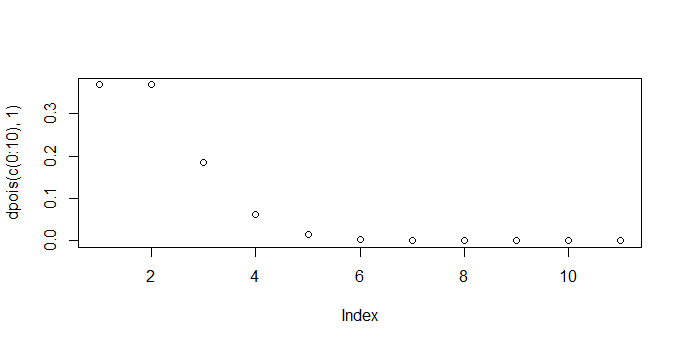
> plot(dpois(c(0:10),2))
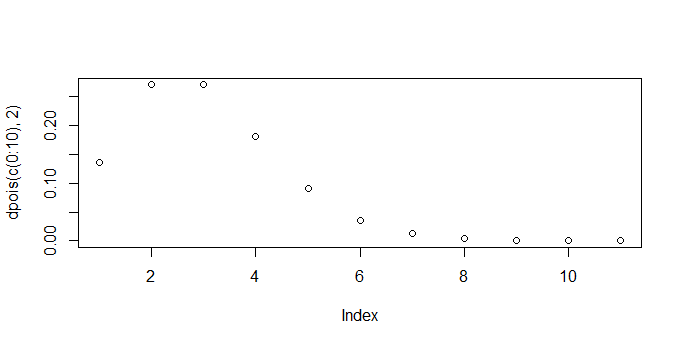
> plot(dpois(c(0:10),3))
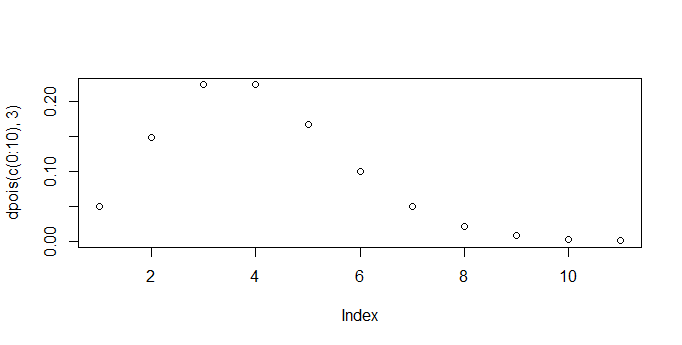
> plot(dpois(c(0:10),5))
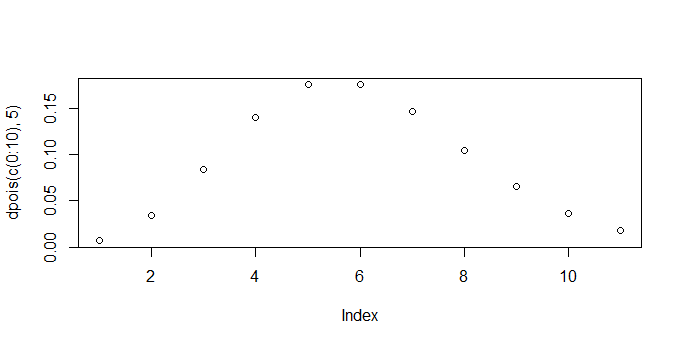
直観的にもあっているように思います。
つまり、平均発生回数付近に山があり、そこから外れるほどに発生する確率が下がっていきます。
また、平均発生回数が大きくなるにつれて分布の分散も大きくなっています。
これも覚えておくとよいポイントですが、分散の値は平均と同じθになります。
θを大きくするとどんなグラフになるの?
θ=50でKが1~100までを描画してみました。
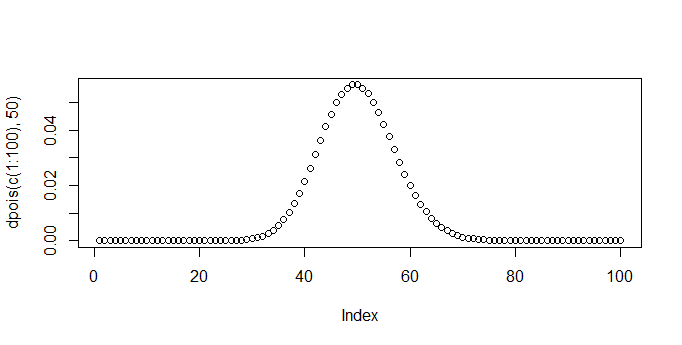
要はθを大きくすればするほど正規分布に近づいてきます。
ポアソン分布は正規分布の特別ケースという側面があります。正規分布は平均だけでなく分散が決まらないと一意に決まりませんが、その近似であるポアソン分布は平均だけで形が決まるのです。
冒頭の1分間に平均2アクセスあるHPに1分間に4アクセスがある確率は何%なの?
先ほどグラフ化した値を取り出します。
> dpois(c(0:10),2) [1] 1.353353e-01 2.706706e-01 2.706706e-01 1.804470e-01 9.022352e-02 [6] 3.608941e-02 1.202980e-02 3.437087e-03 8.592716e-04 1.909493e-04 [11] 3.818985e-0
9.022352e-02
ということで約9%です。
終わりに
ポアソン分布とは、頻繁に起こらない事象を扱う確率分布で、平均事象発生回数のみ分かれば分布の全体を描くことができます。
統計学の初歩としてテーマになることが多い分布なので、知っておくとどこかで役立つと思います。
以上、サルでも分かるポアソン分布入門でした。
