【サルでも分かる】ROC曲線入門（後編）

はじめに

前回までの復習。

• 陽性か陰性かを判断する基準がカットオフ値（カットオフポイント）
• カットオフ値（カットオフポイント）をずらすと真陽性率及び偽陽性率が変わる

ここまでくればROC曲線を理解したも同然です。

いよいよROC曲線

ROC曲線の定義を再掲します

ROC曲線とは、ある検査のカットオフ値を連続的に変化させた際の真陽性率と偽陽性率の値をプロットした曲線

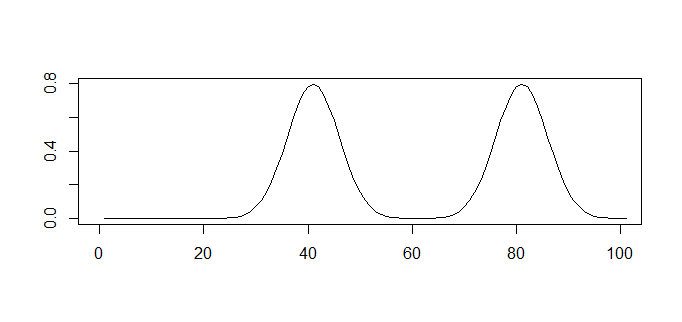
上の検査データを例に、実際に基準である「カットオフ値」をずらしながら偽陽性率と真陽性率をプロットするとどんなグラフになるでしょうか。

1. 検査値が0以上、つまり全てを陽性とするゆるい基準では偽陽性が1で真陽性が1です。
2. そこから基準をあげていけば真陽性率が1のままだんだん偽陽性率が下がってきます。
3. そして検査値が60になると偽陽性率が0、真陽性率が1の完璧な判定基準です。
4. 60を超えて検査値をさらに厳しくしていくと、偽陽性率は0のまま真陽性率がだんだん下がってきます。
5. 最後まで行けば、つまり検査値が100以上ないと陽性ではないとする厳しい基準にしてしまうと偽陽性率も真陽性率も0になります。

つまり、以下のような図になります。

1が右上で3が☆マークで5が左下だね

これがROC曲線です。

ただし、上の例は判定を行う上で最適なケースです。陽性と陰性の分布が綺麗に分かれています。

以下がよくあるケースです。

よく見るROC曲線

陰性の方が以下のような分布で

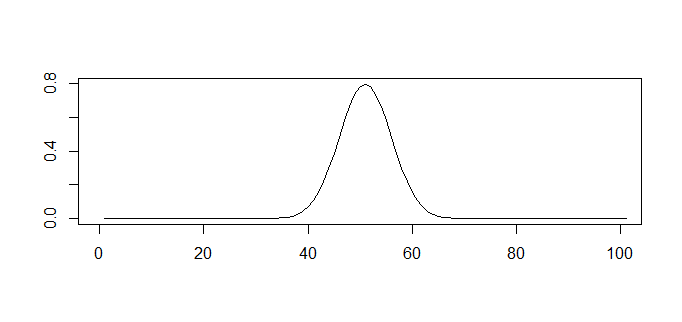
陽性の方が以下のような分布で

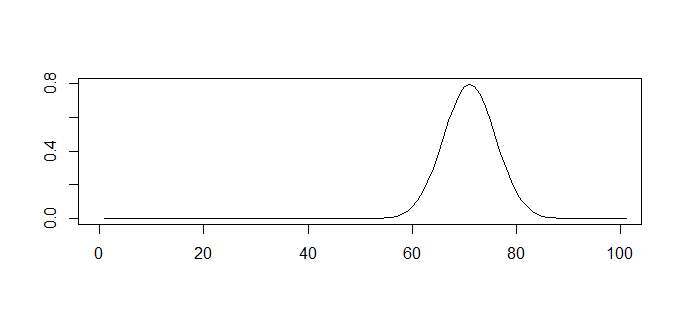
判定するデータが以下のような分布だとします

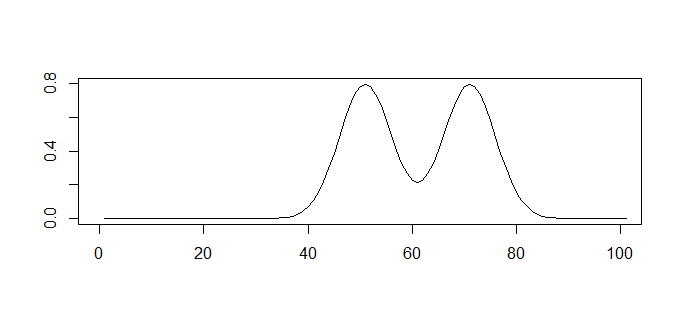
二つの分布が混ざってるね

どこで区切っても、真陽性率を1、偽陽性率を0にすることができないことが分かるでしょうか。
真ん中あたりで区切っても、どうしても陰性の人を陽性としてしまい、どうしても陽性の人を陰性としてしまいます。

ただし、全てを陽性といってしまえば先ほどと同じように真陽性は１に、全てを陰性といってしまえば偽陽性は０です。

このグラフをプロットすると先ほどの直線のようにはいかないことはなんとなくイメージできます。

詳細は割愛しますが、以下のようになります。

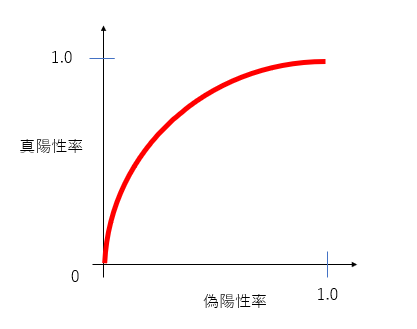
このようにROC曲線は文字通り、曲線を描きながら真陽性率と偽陽性率の関係性を表します。

そして、このROC曲線で囲まれた面積をAUC(Area Under Curve)と呼び、その検出法が最適なROC曲線（以下の図でいう左側）にどのくらい近いかを数値化します。

実際、ROC曲線とはAUCを定量化するために用いられるケースが多く、それは診断法がどれぐらい有用なのかを知る手がかりになります。言わずもがな、ROC曲線が直角であれば精度が高い理想的な診断です。

まとめ

ROC曲線とは偽陽性率と真陽性率が基準値に対してどのように変化するかを示す曲線であり、それを用いて算出されるAUCはその検査がどれくらい有用性があるのかの指標として利用されます。

ちなみに、真陽性率は「感度」と呼ばれたり、偽陽性率に関する値は特異度といった形で表現されることもあります。

統計的精度の評価として、よく登場する曲線なので本記事が理解の一助になれば幸いです。

以上、サルでも分かるROC曲線入門でした。