はじめに
前回までの復習。
- 本当は陰性なのに検査で誤って陽性と判断した割合が偽陽性率
- 陽性を正しく陽性と判断した割合が真陽性率
- 真陽性率は上げたいが偽陽性率は下げたい
いよいよROC曲線の肝であるカットオフ値(カットオフポイント)の説明です。
カットオフポイント?
偽陽性率と真陽性率が分かったので、実際にデータを見ながら考えていきます。
陰性の方を検査した値が以下のような分布だとします。

x軸が検査した値で、y軸が分布です。
値40あたりが平均です。要は、値を検査して40あたりがでれば分布に照らし合わせて「陰性っぽい」と判断できます。
逆に陽性の方を検査した値が以下のような分布だとします。

値80あたりが平均です。
で、実際に検査して判定する際はこのようにごちゃまぜになっています。
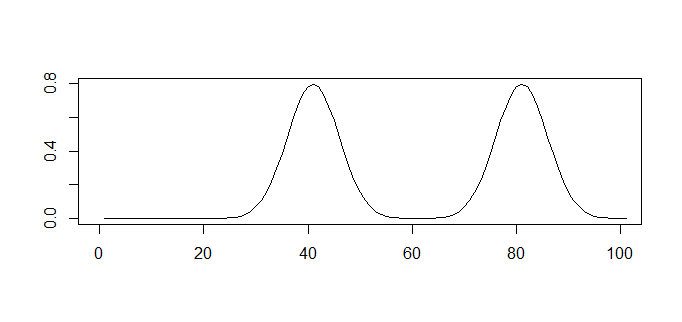
ここから基準値を選定して、陽性か陰性か判断する必要があります。
さて、あなたが判定する立場であれば、どのあたりに線を引くでしょうか?
60あたりで綺麗に分けれそう

みなさん答えは同じで、このあたりだと思います。
検査した値が赤線より高ければ陽性、低ければ陰性。
この検査基準であれば真陽性率は1、偽陽性率が0になります。
そして、検査基準の値をカットオフ値(カットオフポイント)と言います。いわゆる、閾値です。
判定基準の赤線の値がカットオフポイントっていうのか
では、カットオフポイントをずらして見ましょう。
真陽性率と偽陽性率が変化します。
以下のように陽性の基準をゆるくすれば

真陽性率は1のままですが、偽陽性率が大きくなります。
赤線が左側にいくほど陽性の人を陰性と判定することはなくなるけど、陰性の人も陽性と判定しちゃうんだね
逆に以下のように陽性の基準をきつくすれば

偽陽性率は0のままですが、真陽性率が小さくなります。
赤線が右側にいくほど間違って陽性にすることはなくなるけど、陽性の人も陰性と判定しちゃうんだね
カットオフ値を変化させる というイメージが掴めたところでいよいよ以下で最終回です。
