はじめに
本記事では、R言語で可視化しながらカーネルK平均法についてざっくり理解することを目的にしています。
そもそもK平均法とは、通称k-means clusteringと呼ばれるクラスタリング手法です。
クラスタ内のデータの平均値からの距離を元にクラスタ化を収束するまで行います。
シンプルなアルゴリズムですが、以下のように正常に機能します。
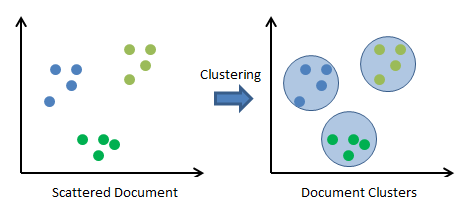
https://www.codeproject.com/Articles/439890/Text-Documents-Clustering-using-K-Means-Algorithm より画像抜粋
ただし、K平均法ではうまく動作しない場合があります。
以下のようなデータです。
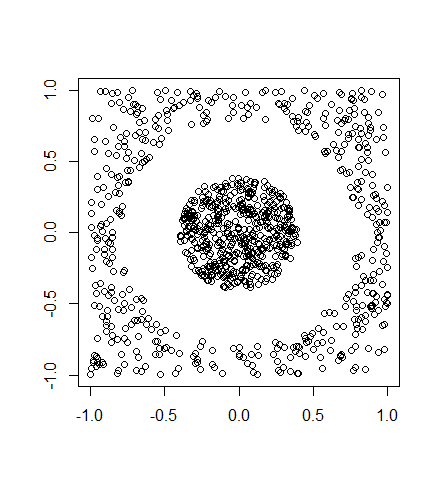
K平均法を使うと以下のように分類されてしまいます。
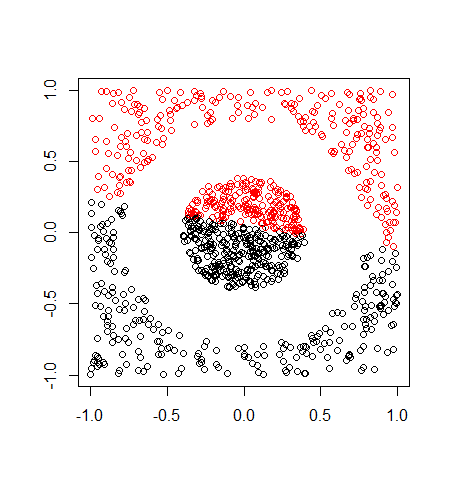
2点間の距離のみで最適化を行うので線形(≒直線的)に分類してしまうのです。
そんな場合に利用できるのが、本記事で説明するカーネルK平均法です。
カーネルK平均法とは?
言葉の定義ですが、カーネルとはカーネル関数から来ています。
カーネル関数とは特定の条件を満たす関数で、データを変換するために利用します。
例えば、上のデータを以下の3次元正規分布の入力に用いるとどうなるでしょうか。
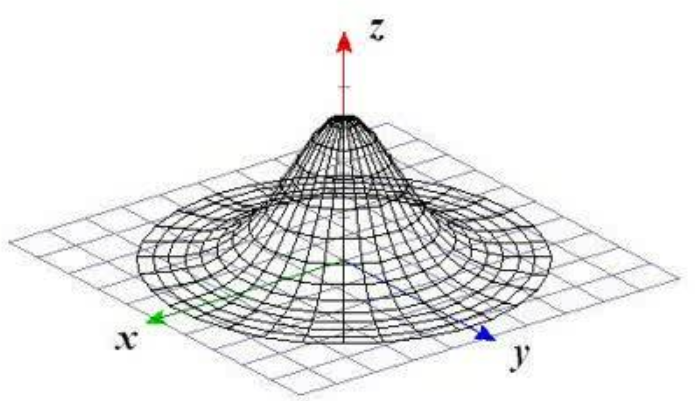
中心に近い値はそのままの値で、外側にあるデータは小さくなりそうです。
図示すると以下のようになります。
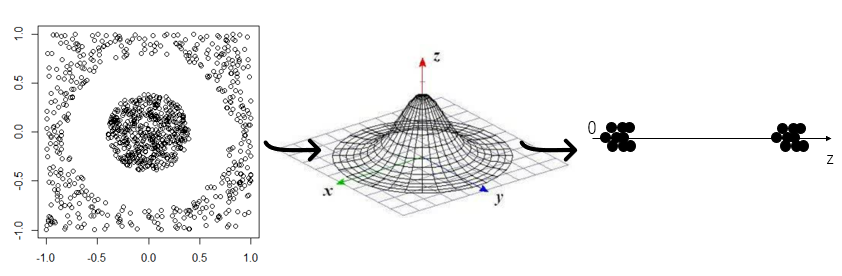
このように、カーネル関数を通した結果に対してK平均法を行うことで直線では分離できないような、いわゆる非線形な分離を行うことができます。
以下が3次元の可視化イメージです。参考になるので添付します。

https://www.youtube.com/watch?v=3liCbRZPrZA の動画内より抜粋
K平均法で分類に失敗した上のデータがカーネルK平均法で分離できるか、R言語でやっていきます。
R言語でカーネルK平均法
R言語でカーネルK平均法はkkmeansで利用できます。
kkmeans(data,N,kernel="XXX")
dataをN個のクラスターにXXXというカーネル関数を用いて分離します。
kernelとして今回使うガウスカーネル(≒正規分布)はrbfdotです。他にも多くのカーネル関数が用意されていますが、本記事では割愛します。
今回利用しているデータは以下のdataです。
> ls(data) [1] "classes" "x"
頭数行を見ると
> head(data$x,n=3) [,1] [,2] [1,] -0.002691136 -0.14930124 [2,] -0.167985116 -0.94717160 [3,] 0.229419227 -0.03829984 > > head(data$classes,n=3) [1] 1 2 1 Levels: 1 2
data$xはx座標とy座標の値、data$classedは分類の正解ラベル(1であれば円の内側、2であれば円の外側)です。
そして以下が正解データによるプロットです。
plot(data$x,col=data$classes,xlab="",ylab="")
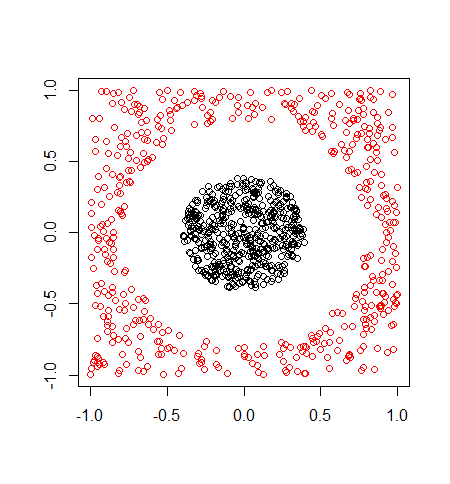
では、kkmeansを使ってラベル付けしてみます。
> kkm <- kkmeans(data$x,2,kernel="rbfdot") Using automatic sigma estimation (sigest) for RBF or laplace kernel
data$xに対してRadial Basis kernel "Gaussian"を利用して2つのクラスに分けました。
頭数行を見ると先ほどと同じクラス分けになっています。
> head(kkm,n=3) [1] 1 2 1
カーネルK平均法で利用した色分けでプロットしても
> plot(data$x,col=kkm,xlab="",ylab="")
ただしく分類できています。
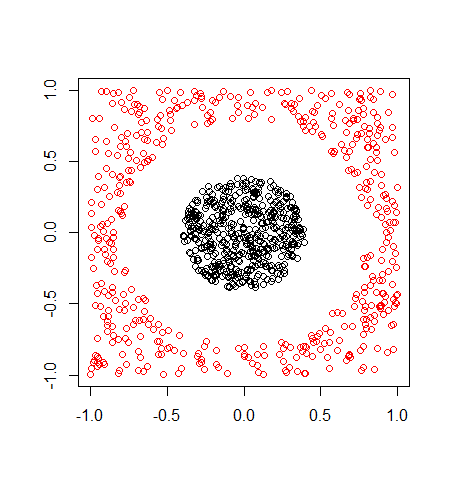
おまけとして、あえてクラスターの数を3,4としてみると以下のような結果になりました。
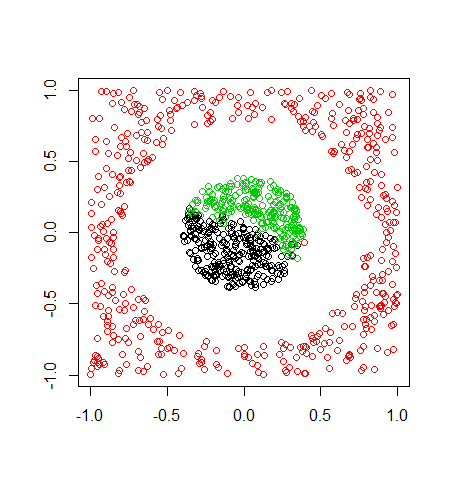
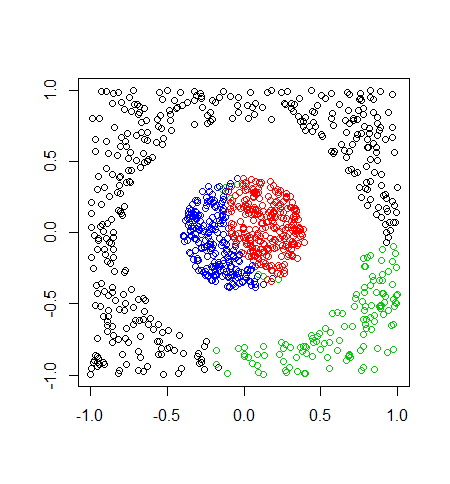
このように分類するクラスター数を正しく入力しないと、カーネルK平均法でも意味のない分類になってしまいます。
まとめ
カーネルK平均法では、線形(≒直線)に分割できないようなデータに対しても一度変換して線形に分割することで、結果的に非線形識別機として動作します。
本記事で、その理解が深まれば幸いです。
以上、カーネルK平均法の入門記事でした。
